
记得中学地理书中说过,“春分、秋分时太阳直射赤道,地球各处昼夜等长”。就是这样一个浅显的道理,在应用到实际情况时,并不是听上去那么简单。在国家授时中心网站可以查到,2009年春分日(3月20日)北京的日出时刻为:06时18分,日没时刻:18时26分,总日长12小时零8分。为什么会这样?
继续阅读
分类目录归档:学海蠡测
话说星期
当月升日沉,晚霞漫天,一天又将逝去,这亘古的昼夜交替带来了最原始的时间观念,“天”理所当然地成为最基本的单位。地球绕太阳一圈需要365天,我们定为一年;月亮绕地球一圈需要30天,我们算做一月,但是为什么要把7天作为一周呢?
神创论者相信这是上帝创世以来的古老习俗,因为圣经中说上帝七天创造世界,第七天上帝休息。在犹太教中周日是一周的开始,于是周六便是用做休息的安息日,西班牙语中周六是Sábado,德语叫Samstag,都是来源于希伯来语中的安息日 Shabbat。基督徒们没有遵从旧约对于安息日的规定,而是在周日纪念耶稣复活,称之为“主日”,法语中的Dimanche,意大利语中的Domenica,都是来自拉丁语中的“主人”这个词- Dominus。但是,根据圣经记载上帝在第二天创造了太阳月亮和星星,为什么第一天是太阳日(Sunday),第二天是月亮日(Monday),后面还用其他星星命名呢?神父们不知道,也不关心,那是“主”的事,现在只要双休就好。
占星师们说,你看夜空中有些星星的位置每天都在变化,它们是金星、木星、水星、火星和土星。加上太阳和月亮,这7颗星合称“七曜”,每日轮流值守,日期就用该日轮值的星名来称呼。但中国古代历法完善,不需要这样一个穿凿附会的7天划分,加上历代帝王一直严禁民间私习星占,“七曜”之术流传不广,倒是日本学了去,沿用至今。
继续阅读
太白小考
星表简介之三-依巴谷

了解天空的奥秘无疑是从星星的位置开始的。早在文字出现之前,人们还在用绘画描述生活场景的时候,就有了对那些明亮光点的记录,这样久远的历史现在已无从考证,战国时期的甘德、石申最早以天文著作闻名,但作品早已失传,只剩名目而已,古希腊喜帕恰斯(Hipparchus)编制的西方第一本星表也是因为被托勒密提及才为世人所知,而托勒密在《天文学大成》中整理的1千多颗恒星在整个中世纪都是权威,这几乎已经是目力的极限,直到17世纪,望远镜发明之后,人类才得以继续拓展自己的视野,随着望远镜口径的不断加大,在二十世纪,我们又走到了光学和机械技术的极限,天文学家们在五十年代前后意识到在地面测定的恒星位置误差主要来自大气的不稳定以及地球运动的不规则,已经很难依靠仪器的进步来解决,只有寄希望于空间望远镜,避开这些干扰因素。
于是法国斯特拉斯堡天文台台长Lacroute在1966年提出了伊巴谷(Hipparcos)计划,全称是高精度视差收集卫星(High Precision Parallax Collecting Satellite),它采用三角视差的方法来测量恒星的位置,距离,运动速度等信息,为了向喜帕恰斯致意而特意凑出了这个发音接近的缩写。在经过近二十年的论证研究之后,欧洲空间局终于在1976年接受了这一方案,着手设计制造。1989年8月8日在法属圭亚那的库鲁(Kourou)由阿丽亚娜4型火箭(Ariane-4)发射升空,本来准备发射到同步轨道上,但在36500公里处时远地点推进器的意外失效使它进入了椭圆轨道,这个轨道离地球最近时只有500km,这虽然高于地球大气(100km),但已经深入了地球辐射带内部,在穿越地球辐射带时,会有大量的高能粒子妨碍正常观测,并逐渐侵蚀着卫星部件,观测时间和使用寿命都受到不小的影响,到了1992年7月卫星开始出现异常,1993年3月在实现了预期的科学目标之后,停止了全部观测活动,1993年8月15日地面控制中心中断了与卫星的通讯联系。伊巴谷卫星从此加入了太空中孤独漫游者的行列。
气压高度计原理
大家都知道水中的压强仅由水深决定,P=ρgh,潜水员可简单的从当前的压强估算出自己的下潜深度。大气压与此类似,是由地表空气的重力所产生的。随着海拔高度的上升,地表的空气厚度减少,气压下降。于是可以通过测量所在地的大气压,与标准值比较而得出高度值,这就是气压高度计的基本工作原理。设海平面处大气压为P0,所在地大气压为P,则海拔高度h=(P0-P)/(ρ*g)。初中课本讲到这里就打住了,但水是液体,密度随温度和压强变化很小,而大气随着海拔高度的增加,温度压强都逐渐降低,导致密度下降,不考虑这一点的公式是没有实用价值的。
假设密度随高度均匀下降,海平面处h=0,ρ=ρ0,大气层外边界处h=r(大气层厚度),ρ=0,故有ρ=ρ0(h0-h)/h0,则海拔h处的大气压是对h0到h处的大气质量求和,因为是线性关系,用等差数列的知识就可以求出海拔h处的大气压应为 P(h)=ρ0(h0-h)^2/(2h0),而海平面处的标准大气压P0和空气密度ρ0均是已知的,取P0=100kPa,空气密度ρ0=1kg/m^3,可由此算出h0=20000米,于是海拔高度的表达式应修正为 h=h0-sqrt(P/P0)。
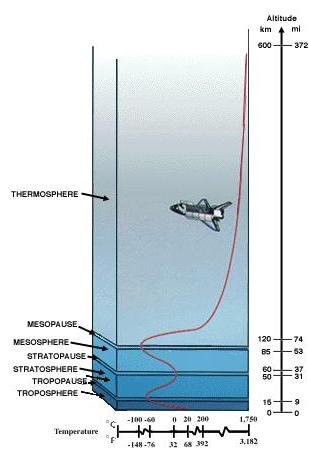
这样算出的海拔是否符合实际还需要更多的数据来检验,不过地球大气的厚度还是很容易查到的,然没有确切的边界,但至少是在500公里以上,而这里给出的估计值只有20公里,问题出在哪里?其实我们的估计并没有错,对地表大气压有贡献的气体厚度确实只有几十公里的量级,更确切的说,大气质量的99%集中在地表30km以内,其中5.6公里内的就占到了50%,100km之上的高层大气虽然对地球环境有重要影响,但其密度已经相当低了。
当然,这种线性关系的假设只是很粗糙的近似而已,由流体静力学平衡条件可以得出,大气密度是随海拔升高呈指数式下降的,不过,这句话也只在大气静态稳定时才近似成立,NASA在此基础上给出了近地大气温度和压力的经验公式,所有的气压式高度计都是利用机械或电路来再现这些气压与高度间的对应关系,但是由于气候变化所造成空气密度差异就完全无法估计了,这是此类高度计的通病。因此在需要高度精确值的场合还是用基于立体几何的GPS好了。
