分类目录归档：学海蠡测

珊瑚化石

4条回复

在一家饰品店看见珊瑚化石做的小挂件，当下心生欢喜，随手考证一番。

因为珊瑚骨骼纹路酷似菊花，也有人称之为菊花石（我最早联想到的其实是柠檬片……），不过这个名字早已用在另一种矿物奇石上了，但那是矿物晶体形成的放射结构，纹理质地都相差很多。国际上的叫法是玛瑙化珊瑚化石(Agatised Fossil Coral)。普通珊瑚的主要成分是碳酸钙，跟家里开水壶底的水垢是同一种东西，硬度较低，但是这种配饰不一样，它有珊瑚的纹理结构，又有玛瑙的质地光泽，到底是怎么来的呢？

其实和硅化木一样，玛瑙珊瑚通常是由于长期处于富含硅酸盐的环境中，原有的碳酸盐被逐渐置换掉，再经历地质作用而变质成岩，这就是所谓的玛瑙化（所以又称菊花玉）。印度尼西亚的一家供应商记录了他们工作的流程，那里的丛林在几千万年前还是浅海大陆架，当年的石灰质珊瑚礁早已风化殆尽，只有致密的玛瑙部分裹在风化壳中存留至今，采石工们挑选出硬度较高，纹理清晰的带回村镇，清洗之后略作分割便放入砖窑烧制，这和玛瑙“烧红”或者陶瓷“釉烧”的原理类似，可以氧化其中的金属离子，使颜色更加鲜艳，最后再切割打磨。就是我现在看到的成品了。类似的东西新疆吐鲁番艾丁湖也有，不过有明显的体壁；而美国福罗里达州的州石玛瑙珊瑚（Agatized Coral）就看不出明显的骨骼花样了，只有类似玉髓的结构。这种差异应该和地质年代、进化历程有关，怎奈珊瑚历史久远，从5亿年前的奥陶纪一直演化至今，名目繁多，我判断不出它们年代和种属，只能有待专业人士了。

英文书法

15条回复

在打字机发明之前，英文也是很讲究书法的，称作calligraphy，意即“漂亮的笔迹”，又因为写得好的多是以誊写为生的penman，也称作penmanship。陀思妥耶夫斯基在《白痴》第三章中有这样的描述：

嗯，这是普通、平常、纯粹的英国字体，不可能写得更优美了，这里真是妙笔生花，精巧玲珑，字字珠矾，可谓笔法高超，而这是变体，又是法国的，我是从一个法国流动推销员那里摹写下来的：还是一种英国字体，但黑线少许浓些，粗些，深些，匀称性被破坏了，您也会发觉，椭圆形也变了，稍稍变圆些，加上采用花体，而花体是最危险的东西！花体要求有不同一般的品味，但只要写得好，只要写得匀称，那么就无与伦比了，甚至还能惹人喜爱。

在古文字学(Paleography)中可将拉丁语系字体演化分为六个阶段： 继续阅读 →

最新物理常数

1条回复

教科书附录中的物理常数实在是太旧了，贴点新的。学界所用的物理常数标准值是由国际科学联合会(ICSU)下设的科技数据委员会CODATA (Committee on Data for Science and Technology)审定给出的，每四年更新一次，最新的一组在今年3月发布，取代了之前使用的2002年推荐值，称作CODATA 2006年推荐值，因为所参考的文献截止到2006年12月31日。审定工作具体由CODATA的基本常数工作组 (CODATA Task Group on Fundamental Constants)承担，结果则是在美国国家标准与技术研究所NIST的物理实验室页面上发布。常用值如下（均为国际单位制，以科学计数法表示，括号中为最后两位对应的误差）：

光速精确值 c = 299 792 458
引力常数 G = 6.674 28(67) e −11
普朗克常数 h = 6.626 068 96(33) e-34
基本电荷 e = 1.602 176 487(40) e −19
电子质量 m_{e} = 9.109 382 15(45) e −31
质子质量 m_{p} = 1.672 621 637(83) e −27
玻尔兹曼常数 k= 1.380 6504(24) e −23
阿伏加德罗常数 N_{A} =6.022 141 79(30) e + 23

其他的导出常数我就不多引了。可以看出，即使和1998年的推荐值相比，也大多只有误差限的变化，对日常使用几乎没有影响。所以说，教科书后的资料老一点其实也没什么关系，但是连出处都没有的数据，又叫人怎么用着放心呢？如果对方法感兴趣可以参考2002年数值修订的工作评述 CODATA Recommended Values of the Fundamental Physical Constants: 2002, by P. J. Mohr and B. N. Taylor, Reviews of Modern Physics Vol. 77, No. 1, pp 1-107 (2005)。

掌舵问题

2条回复

记得在高中物理中有这样一道习题，“一条速度为v的小船要过河，所需的最短时间和最短路程分别是多少，设水速为c，河宽为D”，答案很简单：最短时间不要求靠岸的位置，船头正对河岸即可；最短路程显然就是垂直距离（要求v>a），典型的速度矢量合成；而对v小于a的情况讨论则是学科竞赛的要求了，问题等效于已知三角形的两条边求使其中短边所对角最小的三角形，这个干净的几何解法让我对物理学的优美有了直观而深刻的印象。后来上了大学，在高等数学中（同济第四版）又见到同样的情景，求的是船头始终指向对岸目的地时的航线轨迹，因为船只位置在变，船头方向也在一直调整，据此建立微分方程组，不难解出迹线方程，不久后接触了数学建模，便不再囿于那些过于简化的题设了……

现实生活中的行船从来不是课本中所描述的那样简单，码头的位置是固定的，航向可以随时改变，水流的速度与河岸距离有关……这时再问同一个问题:“小船怎样过河时间最短？”，没人能轻易给出答案。
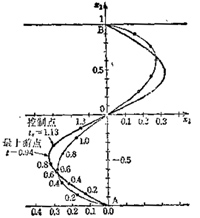最短时间航线设码头在正对岸，这是个变分问题，但不能用常规办法求解，我在这里卡住很久，直到最近才在近藤次郎的《数学模型》一书中发现了解法，数值解；用的是前苏联数学家庞特里亚金1956年发表的最大值原理，该原理广泛应用于宇宙航行的轨道计算，但是同其它近代数学的进展一样，没有一个简单直观的表述，有兴趣的朋友请自行查阅。得出的航行轨迹如右图所示(图中两条线代表两种不同的控制方式)。最少燃料策略则与最短时间策略稍有不同，虽然都出乎我的意料，倒也不难理解，在水流较缓的岸边逆流而上调整航线，在水流湍急的河心顺流直下争取时间。

几年的困扰至此总算告一段落，现在我倒想听听内河船长们的经验，也许会有更多的选择

仔细想想，如此循序渐进的教法无非是要回避困难问题所带来的挫败，但这样建立起来的自信在现实面前不堪一击，没有探索的动力，没有发现的乐趣，什么样的孩子会喜欢这样的学习？社会期待创造力，而好学生往往只是听话而已。记得在William F.Lucas在《微分方程模型》(国防科大应用数学模型丛书)中曾说：“本章的目的是教你如何解决问题，而不是显示有人能够做什么！”